티스토리 뷰
이 글은 David Silver의 강화학습 강의자료를 기초로 하였으며 아래의 강의를 듣고 작성하였습니다.
https://www.youtube.com/watch?v=NMesGSXr8H4&list=PLpRS2w0xWHTcTZyyX8LMmtbcMXpd3s4TU&index=2
https://www.davidsilver.uk/teaching/
Teaching - David Silver
www.davidsilver.uk
MP, MDP, MRP, MDP에서의 value function과 optimal value function, policy에 대해서
■ 1. Markov Processes
● MDP
- 강화학습에서 environment를 표현
- environment가 완전히 관찰가능한 상황
- 현재 state가 process를 완전히 표현한 것
- 거의 모든 강화학습 문제는 MDP문제로 만들 수 있다.
(e.g optimal control, partially obervable problems, Bandits)
● Markov Property
P[St+1|St] = P[St+1|S1...St]
- state가 모든 관련 정보(history)를 알고 있어 history를 던져 버릴 수 있다.
- state는 function의 충분 통계량
● State Transition Matrix


- 현재 sate에서 각 state로 전이할 확률을 Matrix (state가 n개)
- 각 row의 합은 1
● Markov Process : (S, P)
- memoryless random process(memoryless : 어느 경로로 왔든 관계없이, 온 순간 미래가 정해짐, random : sampling 할 수 있다.)
- Markov property를 가지는 random state들의 sequence
- Environment의 dynamics에 관한 것
- S : state들의 집합 (n개 discrite)
P : state들의 전이확률 매트릭스

■ 2. Markov Reward Processes
(S, P, R, γ)
- S : state들의 집합 (n개 discrite)
P : state들의 전이확률 매트릭스
R : reward function Rs = E[Rt+1|St=s]
γ : discount factor, γ∈ [0, 1]
- Edge에다 reward 줄 수 있나?
- reward process에서는 action이 없음, 확률적으로 길을 가는 것! state에 도달하면 가는 것!
- action을 강화시키려면 action에다 reward를 주면 되는데 확률적으로 가는 것이므로 state에만 reward를 준다.

● Return
- Return(Gt) : 경로들 sampling할 때 미래의 reward를 감가상각 하여 reward를 더한 것(cumlative discount reward)
- γ가 0에 가까울수록 'myopic'(근시안적, 순간적 reward만 중요), γ가 1에 가까울수록 'far-sighted'
- cumlative discount reward(Return)를 maximize하는 것이 강화학습의 목적
- discount하는 이유는 수리적으로 편리해서(discount 덕분에 수렴),
만약 모든 sequence가 종료하는 게 보장된다면 에피소드를 샘플링할 때 γ를 1로 해도 될 때가 있다.

● Value Function
- Value Function(v(s)) : Return의 기대값
v(s) = E[Gt | St = s]
- 샘플링하여 에피소드를 만들고 에피소드마다 reward를 만듦.
- 같은 시작점이어도 어떻게 샘플링하느냐에 따라 Return 값이 달라짐. 그것의 평균
- 기대값을 사용하는 이유 : 미래는 불확실하므로, 그것을 모두 반영
e.g) Student MRP 예제

● Bellman Equation for MRPs :
- 즉각적인 Reward Rt+1
- discounted value of successor state γv(St+1)
- s에서의 value는 현재 state의 Reward와 (현재 state에서 다음 특정 state로 갈 확률*그 state로 갔을 때 reward의 합)
- Law of Iterative expectation 사용 E[Gt+1 | St+1] = vSt+1


e.g) Student MRP 예제(p15)

- Bellman Equation의 Matrix Form
- Bellman Equation은 linear equation. It can be solved directly(아래 테이블 오른쪽)
- Direct solution은 계산 복잡도가 커(O(n3)) 작은 MRPs에서만 가능하다
- large MRPs에 대해서도 Dynamic Programing / Monte-Carlo evaluation / Temporal-Diffrence learning을 적용하여 가능하게 할 수 있다.
| Bellman Equation Matrix Form | Direct Solution |
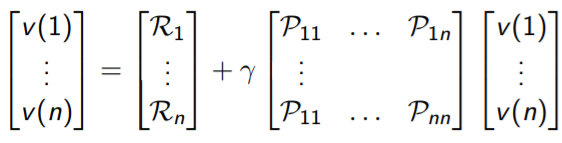 |
 |
■ 3. Markov Decision Processes
(S, A, P, R, γ)
- S : state들의 집합 (n개 discrite)
A : action들의 집합
P : state들의 전이확률 매트릭스
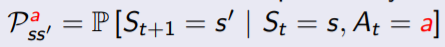
R : reward function

γ : discount factor, γ∈ [0, 1]
- state가 중요하지 않고 action마다 reward가 주어짐. action을 한다고 무조건 어떤 state로 가는 것이 아니라 action을 하면 그 action에서 확률적으로 state를 가게 된다. environment를 결정
- model-based = state model + reward model
- 장점 : planning 가능(미리 변화를 예상 후 최적의 행동 계획 가능)
- 단점 : 실제 environment의 정확한 model을 알아내기 어려움/불가능 →
e.g) Student MDPs

● Policies (π)
- 어떤 정책을 갖고 action을 할지가 중요하다. action을 할 확률
π(a|s) = P[At = a | St = s]
- agent의 행동을 완전히 결정
- MDP에서 policy는 현재 state대해서만 의존(not the history)
- Policy는 stationary(time-independent)
- agent의 Policy가 고정하면 State는 Markov process가 된다.
(Policy가 고정되면 어떤 state에 있을 때 다음 state를 갈 확률을 계산할 수 있음(그 state에서 action할 확률 그 action으로 s→s'갈 확률 곱하는))
- State와 reward sequence는 Markov reward process라 할 수 있다.

● Value Function(v(s)) : Return의 기대값
- 어떤 state에서 policy를 따라 에피소드가 끝날 때까지 계속 게임했을 때 여러 개를 샘플링했을 때 평균
- 알파고가 한 방법
(1) state-value function
vπ(s) = Eπ[Gt | St = s]
(2) action-value function
qπ(s, a) = Eπ[Gt | St = s, At = a]
- Bellman Expectation Equation:
(1) state-value function : 일단 한 state를 가고 그 다음 state부터 policy(π)를 따라 감

(2) action-value function : state에서 action을 하여 reward를 받고 다음 state에서 다음 action을 하는 기대값

- Vπ : state(s)에서 action(a)를 했을 때 policy(π)를 따라 게임을 끝까지 하면 얻을 return의 기대값(action-value function의 가중치 합, 한 스텝을 간 것이 아니라 γ가 없음)
- Qπ : action의 value function, state(s)에서 action(a)를 했을 때 Reward를 갖고, 다음 각 state들(s')에 떨어질 확률에 value function을 더한 것 (*γ : discount factor)
- 하얀 원은 state, 검은 원은 action
| Vπ에 대한 Bellman Expectation Equation | Qπ에 대한 Bellman Expectation Equation |
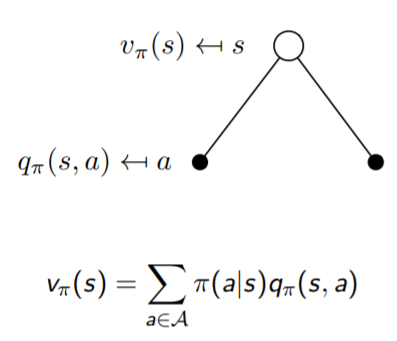 |
 |
 |
 |
e.g) Student MDP
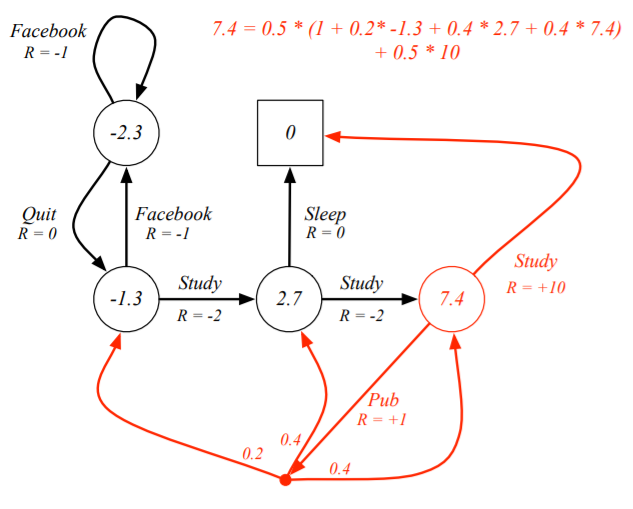
● Bellman Expectation Equation의 Matrix Form
| Bellman Equation Matrix Form | Direct Solution |
● Optimal Value Fuction
(1) Optimal state-value function : 모든 가능한 policy 중에 maximum value에 대한 함수

(2) Optimal action-value function : 모든 가능한 policy 중에 q함수(action-value function)이 maximum

e.g) Optimal value function / Action-value function for Student MDP
| Optimal Action=Value Function | |
study = 10 / pub = 2.39 가장 큰 값 선택  |
 |
● Optimal Policy
- 두 policy 중 하나가 나은지 비교 법 - "partial ordering"
- partial ordering : 어떤 policy 두 개를 줬을 때 항상 비교할 수 있는 것은 아니나, 어떤 두 개 중 하나가 낫다고 할 수 있는 경우가 존재(모든 state들에 대해서 Vπ가 Vπ'보다 나을 때)

- 모든 MDP들에 대해서
(1) optimal policy π*가 존재하며, 이것은 다른 policy들보다 같거나 더 낫다 (π* ≥π, ∀π)
(2) 모든 optimal policy들을 따르면 optimal value function과 같다.

(3) 모든 optimal policy들을 따르면 optimal action-value function과 같다.

- optimal q인 q*(S, a)를 알면 우리는 optimal policy를 갖는다.

- 모든 MDP문제에서는 policy는 본디 stochastic(각 action에 대한 확률을 알려주는)나, 위의 경우 무조건 그 state에서 그 action을 하는 것이므로 deterministic optimal policy가 존재한다.
e.g) 가위바위보게임에서 주먹을 50%확률을 낸다고 할 때, 거기서 deterministic optimal policy는 보만 내는 것
e.g) Optimal Policy for Student MDP

● Bellman Optimality Equation for V* / Q*
- Bellman equation : recursive하게 한 step 넘어간 것을 v와 q를 이용해 표현
- Bellman optimality equation는 non-linear
- iterative solution 방법으로 value iteration, policy iteration, Q-learning, Sarsa(뒤에 강의)가 있다.
| V*에 대한 Bellman Optimality Equation | Q*에 대한 Bellman Optimality Equation |
 |
 |
 |
 |
e.g) Bellman Optimality Equation for Student MDP

'Data Science&AI' 카테고리의 다른 글
| [강화학습 뿌시기] 4. Model-Free Prediction (1) | 2022.01.24 |
|---|---|
| [강화학습 뿌시기] 3. Planning by Dynamic Programming (0) | 2022.01.08 |
| [강화학습 뿌시기] 1. 강화학습(Reinforcement Learning) 기초 (0) | 2022.01.06 |
| [논문리뷰]Tabular Data : DeepLearning is Not All You Need (0) | 2021.07.28 |
| [머신러닝 기초] Bagging(배깅) vs Boosting(부스팅) (0) | 2021.07.17 |
- Total
- Today
- Yesterday
- 데이터 드리프트
- SQLD
- SQLD자격증
- amzaon quicksight
- 시계열딥러닝
- NHITS설명
- 오토인코더
- SQLD 정리
- data drift
- 영화 인턴
- Model Drift Detection
- 영어공부
- 생성형BI
- Model Drift
- Generative BI
- 추천시스템
- Tableau vs QuickSight
- On-premise BI vs Cloud BI
- 비즈니스 관점 AI
- 모델 배포
- amazon Q
- 모델 드리프트
- 모델 드리프트 대응법
- Data Drift와 Concept Drift 차이
- Concept Drift
- pandas-ai
- 최신시계열
- Data Drift Detection
- pandas-gpt
- AutoEncoder
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 27 | 28 | 29 | 30 |