티스토리 뷰
이 글은 David Silver의 강화학습 강의자료를 기초로 하였으며 아래의 강의를 듣고 작성하였습니다.
https://www.youtube.com/watch?v=47FyZtBRglI
https://www.davidsilver.uk/teaching/
Teaching - David Silver
www.davidsilver.uk
Model-Free(Environments, transition, Reward를 모를 때) Prediction
Policy Evaluation - MC / TD
■ Introduction
● Model-Free Reinforcement Learning
(지난 강의 요약) MDP를 알 때, Prediction/Control 문제 풀었다.(Planning by dynamic programming)
- Prediction : 주어진 policy에 대하여 value function을 찾는 것
(↔ Control : 더 나은 policy를 찾는 것)
- Model-Free : MDP에 대한 정보를 모르는 상황
▶Model-Free Prediction : MDP를 모를 때(Environment가 어떻게 동작하는지(transition matrix, reward) 모르는 것, )
value function 학습
■ Monte-Carlo Learning
● Monte-Carlo Reinforcement Learning
- Monte-Carlo : 직접 풀기 어려운 것을, 사건을 실제 실행하며 나온 실제값으로 추정하는 것, 그냥 해보는 것!
- MC는
(1) 경험으로부터 직접 배운다.
(2) Model-Free!(MDP의 transition과 reward를 몰라도 policy에 따라 하면 된다.)
(3) 에피소드가 끝나야 return이 정해진다.(All episodes must terminate)
(4) no bootstrapping
- Environment 내에서 agent가 주어진 Policy에 따라서 움직이며 value function은 어떤 state 있을 때 이 state로부터
게임 끝날 때까지 얻을 return의 기대값을 구하는 것
- MC에서 Value = return들의 평균
(* return정의 : 게임 끝날때까지 얻은 reward들의 cumulative sum(discount적용)
● Monte-Carlo Policy Evaluation
- 목적 : policy π에 따라 experience의 에피소드로부터 vπ를 학습하는 것 (S1, A1, R2, ..., Sk ~ π)
- return : total discounted reward

- value function : expected return(return은 확률값)

- Monte-carlo policy evaluation는 expected return 대신에 empirical mean return을 사용
(1) First-Visit Monte-Carlo Policy Evaluation
- state마다 하나씩 칸이 있는 테이블이 있고 방문할 때마다 counter을 하나씩 늘리고,
게임 끝날 때 얻는 return을 그칸에 적으면,
- 처음 방문할 때만 counter를 늘리고, return을 더한다.
- state s가 한 episode에 방문한 처음 time-step t
- Counter : N(s) ← N(s) + 1
- Total Return : S(s) ← S(s) + Gt
- Value(mean return) : V(s) = S(s)/N(s)
- 큰 수의 법칙에 따라, V(s) → vπ(s) (as N(s) → ∞)
(2) Every-Visit Monte-Carlo Policy Evaluation
- state를 방문할 때마다 counter를 올려줌
- Every time-step t that state s is visited in an episode
- Counter : N(s) ← N(s) + 1
- Total Return : S(s) ← S(s) + Gt
- Value(mean return) : V(s) = S(s)/N(s)
- 큰 수의 법칙에 따라, V(s) → vπ(s) (as N(s) → ∞)
- 모든 state들을 평가하는 게 목적이나 모든 state들을 방문한다는 가정해야! Policy가 골고루 움직일 수 있어
- 큰 수의 법칙에 따라 두 개 결과 같음
● Incremental Monte-Carol Updates
| Incremental Mean | Incremental Monte-Carlo Updates |
 |
- V(s) Update (incrementally after episode S1, A1, R2, ..., ST) - 각 State St , Return Gt에서 (이전 value에다 현재 나온 error term만큼 업데이트)  - N이 계속 커지는데 α로 고정 가능 - 오래된 기억들은 잊어 버리는 것! - non-stationary 문제에서 좋을 것!(MDP가 조금씩 바뀌는 것) |
■ Temporal-Difference Learning
● Temporal-Diffence Learning
- TD는
(1) 경험으로부터 직접 배운다.
(2) model-free!(MDP의 transition과 reward를 몰라도 policy에 따라 하면 됨)
(3) 에피소드가 끝나지 않아도 배울 수 있다. (Incomplete episodes, by bootstrapping)
- "TD updates a guess towards a guess (한 스텝 가서의 guess로 guess를 업데이트)"
● MC and TD
- 목적 : learn vπ online from experience under policy π
- MC ; actual return Gt쪽으로 V(St)를 업데이트
- TD ; estimated return(아래식의 TD target) 쪽으로 V(St)를 업데이트
- 끝까지 가기 전에 예측으로 state를 업데이트를 해버림, 순간적인 차이(temporal-difference)로 업데이트
- TD target : 한 스텝을 가서 그 스텝에서 추측을 하는 것이 V(St+1), 그 과정에서 받은 Reward Rt+1
- 그 값으로 V(St)를 업데이트

e.g) Driving Home Example (Total Time 예측)
| 지금까지 경과시간 / 앞으로 예상시간 / 도착 총 예정 시간 | Monte Carlo methods | TD methods |
 |
 각 state를 43분으로 업데이트 |
 매 스텝마다 내가 예측하는 시간이 달랐음. 다음 state값으로 업데이트! |
● MC vs TD 장단점
| Monte Carlo methods | TD methods | |
| 특징 | - 에피소드가 끝날 때까지 기다렸다가 끝날 때 얻는 return값으로 업데이트 - complete sequences로 학습 - 오직 terminating environments에서 학습 |
- final outcome이 나오기 전에 학습 - 매 step 후에 online 학습 - continuing(non-terminating, incomplete sequences) environments에서 학습 |
| 장점 | - 수렴 성질이 좋음 - function approximation - Neural Net을 써도 수렴 성질이 좋음 - 이해하고 사용하기 간단함 |
- 주로 MC보다 효율적 - TD(0)는 Vπ(S)에 수렴 (function approximation일 때만이 아니라) |
| Var, Bias | High variance, zero bias | Low variance, some bias |
| 초기값 민감여부 |
초기값에 매우 민감하지 않음 | 초기값에 더 민감 |
| Markov Property |
Markov property를 사용하지 않음 (주로 non-Markov environments에서 더 효율적) |
Markov property를 사용해서 추측 (주로 Markov environments에서 효율적) |
💡 Bias / Variance Trade-Off
◾ Bias
- Return Gt 아래식은 Vπ(St)의 불편추정량

- True TD Target 아래 식은 Vπ(St)의 불편추정량이나 TD target은 Vπ(St)의 biased 추정량

◾ Variance
- TD Target은 return보다 variance가 훨씬 낮다.
- Return: 많은 랜덤 actions, transitions, rewards에 의존
- TD target : 하나의 랜덤 action, transition, reward에 의존
● Batch MC and TD
- K개의 제한된 에피소드가 있다고 가정. sample episode k∈[1, K], MC와 TD는 같은 값에 수렴할까?
(* V(s) → vπ(s) (experience → ∞)

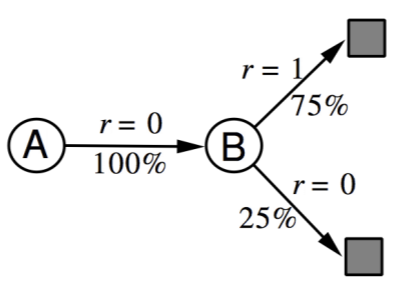
- e.g) 2 states A,B / no discounting / 8 episodes of experience
V(B) = 0.75(6/8가 1), V(A) = ? (사례가 적음)
| A,0,B,0(Astate 시작, reward 0받고 Bstate로 갔다 reward0 받고 끝난 에피소드) B,1 (두번째 에피소드는 Bstate에서 시작해서 reward1을 받고 끝남) B,1 B,1 B,1 B,1 B,1 B,0 |
 |
● Certainty Equivalence
- MC : mse(mean-sqaured error) 최소값을 가진 solution으로 converge
(e.g. AB 예제에서, V(A) = 0)
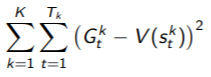
- TD(0) : likelihood Markov model의 최대값을 가진 solution으로 converge
(e.g. AB 예제에서, V(B) = 0.75)
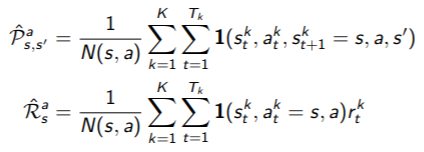
● Monte-Carlo Backup / Temporal-Difference Backup / Dynamic Programming Backup
- MDP를 알 때, DP hybrid 가능 / MDP를 모를 때 갈 수 있는 어떤 state들이 있는 지 모르니까 DP를 못함
| Monte-Carlo Backup | Temporal-Difference Backup | Dynamic Programming Backup |
| - Tree 처럼 가서 value 업데이트 - 알파고에 쓰임  |
- 추측치로 추측치를 바로 업데이트 - Bootstrapping이라고 함  |
- 이 칸에서 할 수 있는 모든 action에 대해서 한 step 가보며 value 업데이트 - full sweep  |
● Bootstrapping & Sampling
◾ Bootstrapping : estimate가 포함되어 업데이트 (depth관점)
▫ MC : bootstrap X (끝까지 가니까)
▫ DP : bootstrap (한 step만가고 멈추니까)
▫ TD : bootstrap (한 step만가고 멈추니까)
◾ Sampling : 샘플들의 기대값으로 업데이트 (width관점)
▫ MC : samples (했던 걸로 해보니는 거니까)
▫ DP : samples X (거기서 가능한 모든 action들을 다 해보니까)
▫ TD : samples (했던 걸로 해보니는 거니까)
● Unified View of Reinforcement Learning
- bootstrapping(shallow backups(Bootstrap)) / Sampling(sample backups) 하느냐!
- full backups - 모델을 알 때
- Exhaustive search : 다 해보는 거!

■ TD(λ)
● n-Step Prediction
- TD target은 한 스텝만 가서 예측할 수도 있고, 미래에 n스텝 가서 예측할 수 있다.
- 무한히 가면 Monte carlo

● n-Step Return
◾ n-step Return
- St+n : estimate

◾ n-step temporal-diffence learning
- 위에 식 값이 정답 자리에 들어와, n-step TD error!

● Averaging n-Step Return
◾ 다른 두 step의 정보를 합친다.
(e.g. 2-step & 4-step returns : 1/2G(2) + 1/2G(4))
◾ Forward view TD(λ) (λ-return)
- 모든 n-step return을 합친다.
- gemetric mean을 사용(memoryless하게 학습, TD(0)과 같은 비용으로 TD(λ) 학습 가능)
- λ는 0과 1사이이므로 MC로 갈수록 가중치가 적어짐
- 미래를 보고 업데이트
- MC와 마찬가지로, episode가 끝내야 계산가능

◾ Backward view TD(λ)
- online으로 매 스텝 업데이트(끝나지 않아도 가능)
- Eligibility(적격) Traces(Et(s)) : 책임을 어디에 물어야 하나?
- frequency heuristic(빈도수) / recency heuristic(가장 최근) 둘을 합친 것!
- 방문할 때 1, 방문하지 않으면 0
- TD-error δ(t) & Eligibility trace만큼 업데이트
- λ = 0 : 오직 현 state만 업데이트 (= TD(0))
- λ = 1 : (= MC)

● Sum of offline updates ← forward-view & barward-view TD(λ)
- Online update : 학습 하면서 환경에서 움직이는 것
- Offline update : 다 움직인 다음에 학습

'Data Science&AI' 카테고리의 다른 글
| [강화학습 논문리뷰] DQN(Deep Q-Network) 소개 (0) | 2022.02.09 |
|---|---|
| [강화학습 뿌시기] 5. Model Free Control (0) | 2022.02.01 |
| [강화학습 뿌시기] 3. Planning by Dynamic Programming (0) | 2022.01.08 |
| [강화학습 뿌시기] 2. Markov Decision Processes(MDP) (0) | 2022.01.07 |
| [강화학습 뿌시기] 1. 강화학습(Reinforcement Learning) 기초 (0) | 2022.01.06 |
- Total
- Today
- Yesterday
- NHITS설명
- 영어공부
- Concept Drift
- 모델 드리프트 대응법
- 시계열딥러닝
- pandas-gpt
- Data Drift Detection
- 추천시스템
- 데이터 드리프트
- 비즈니스 관점 AI
- Data Drift와 Concept Drift 차이
- Generative BI
- pandas-ai
- 오토인코더
- 생성형BI
- 모델 배포
- Model Drift
- amzaon quicksight
- 최신시계열
- On-premise BI vs Cloud BI
- Model Drift Detection
- AutoEncoder
- data drift
- amazon Q
- Tableau vs QuickSight
- SQLD
- 모델 드리프트
- SQLD 정리
- SQLD자격증
- 영화 인턴
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 27 | 28 | 29 | 30 |

