티스토리 뷰
이 글은 David Silver의 강화학습 강의자료를 기초로 하였으며 아래의 강의를 듣고 작성하였습니다.
https://www.youtube.com/watch?v=2h-FD3e1YgQ&list=PLpRS2w0xWHTcTZyyX8LMmtbcMXpd3s4TU&index=5
https://www.davidsilver.uk/teaching/
Teaching - David Silver
www.davidsilver.uk
Control : 최적의 policy를 찾는 것 (Model Free)
On-Policy Monte-Carlo Control / On-Policy Temporal-Difference Control (Sarsa)
Off-Policy Learning (Importance Sampling Q-Learning)
■ Introduction
● Model-Free Prediction
(지난 강의 요약) MDP에 대해 value function 측정
■ On-Policy Monte-Carlo Control
● Model-Free Control 사용예
- 엘레베이터 알고리즘, Robocup 축구, 포트폴리오 management 등
- MDP를 모르거나 sampling을 할 수 있을 때, MDP를 알지만 sampling하기 어려울 때
● On and Off-Policy Learning
◼ On-policy Learning ("Learn on the job")
- 최적화하고자 하는 policy = behaviour policy(실제 environment에서 경험을 쌓는 policy)
- policy π에 대해 π에서 샘플링된 경험으로부터 학습
- e.g. 알파고
◼ Off-policy Learning ("Look over someone's shoulder")
- 최적화하고자 하는 policy ≠ behaviour policy(실제 environment에서 경험을 쌓는 policy)
- 최적화하고 싶은 policy가 아닌 다른 agent의 경험을 이용
- policy π에 대해 μ에서 샘플링된 경험으로부터 학습
● Generalised Policy Iteration with Monte-Carlo Evaluation
◼ Policy evaluation : Monte-Carlo evaluation V = vπ/ Policy improvement : Greedy policy improvement
- No!! Monte Carlo로 V학습. V로 바탕으로 greedy policy를 한다는 것은
현재 state가 있고 다음 state가 뭔지 알 때, 그 다음 state의 v값 중 제일 v값이 큰 값으로 가는 policy를 만드는 것
- 다음 state를 안다는 것은 MDP를 안다는 것! MDP를 모를 때는 가보지 않고는 다음 state가 뭔지 모름
- V만 학습해서는 greedy하게 policy를 improve할 수 없음 (policy evaluation은 할 수 있으나)
◼ Model-Free Policy Iteration Using Action-Value Function
- MDP의 모델을 알아야 V(s)에 대해 greedy policy improvement를 할 수 있음 (State-value function)
- Action-value function을 학습 Q(s, a)에 대해 greedy policy improvement는 가능? O
- 다음 state의 reward를 모르지만, Q는 Monte-Carlo법칙으로 구할 수 있음
- state s에서 action a를 취했을 때 나온 return들의 평균을 취함
- state s에서 취할 수 있는 action이 무엇인지는 아니까 할 수 있는 action 중 Q값이 높은 것을 취함

▶▶ Policy evaluation : Monte-Carlo policy evaluation Q = qπ/ Policy improvement : Greedy policy improvement
- 문제는... greedy policy improvement는 모든 state를 다 충분히 봐야하는데,
막힐 수 있음('You can stuck'). exploration이 안 됨 (reward가 높은 한 쪽으로만 치우칠 수 있음)
◼ ε-Greedy Exploration
- policy improvement 할 때 간단한 아이디어로 exploration을 보장해주는 것
- ε(아주 작은 확률)확률로 랜덤하게 다른 action을 선택
- 1-ε의 확률로 제일 좋은 action(greedy action)을 선택
- 모든 action(m개의 actions)에 대한 explore함을 보장

◼ ε-Greedy Policy Improvement
- 어떤 ε-greedy policy π에 대해, qπ에 관해서 ε-greedy policy π' 는 improvement한다. (Vπ'(s) ≥ Vπ(s))
- 현재 action은 π'(ε-greedy policy)으로 선택, 이후에는 π를 따라갔을 때 value

▶▶ Policy evaluation : Monte-Carlo policy evaluation Q = qπ/ Policy improvement : ε-Greedy policy improvement

◼ Monte-Carlo Control
- Monte-Carlo로 policy evaluation할 때 episode단위로 evaluation, value update.
- 딱 한 episode만 쌓아 Monte-Carlo evaluation하고, 바로 ε-greedy improvement 단계로!
▶▶ Every Episode
Policy evaluation : Monte-Carlo policy evaluation Q ≈ qπ/ Policy improvement : ε-Greedy policy improvement
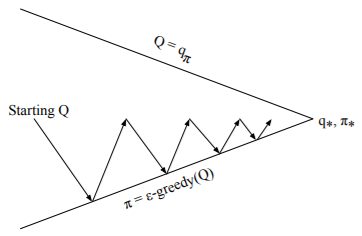
◼ GLIE(Greedy in the Limit with Infinite Exploration) 조건을 만족시키는 Monte Carlo Control
▫ GLIE
- (exploration) 모든 state-action pair들이 무한히 많이 반복되어야 한다.

- (exploitation) policy는 greedy-policy로 수렴한다.
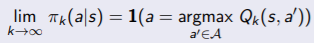
- 예를 들면, εk = 1/k, ε은 계속 줄어든다.
▫ GLIE Monte-Carlo Control
- π를 사용한 k번째 샘플 episode : {S1, A1, R2, ..., ST} ~ π
- (evaluation) episode에서 각 state St와 action At

- (improvement) 새로운 action-value function으로 policy을 improve

▫ GLIE Monte-Carlo Control는 optimal action-value function에 수렴(Q(s, a) → q*(s, a))
■ On-Policy Temporal-Difference Control
● MC vs TD Control
◼ Temporal-difference(TD) Learning
- variance가 작고, online 학습(episode가 안 끝나도 학습 가능), incomplete sequences에서도 학습
◼ Contol loop에서 MC 대신에 TD?
- Q(S, A)에 TD 적용, ε-greedy policy improvement 사용, 매 time-step에서 업데이트
● On-Policy Control with Sarsa
◼ Sarsa
- state s에서 action a를 하고 reward r을 받은 후, s' state로 가서 action a'
- state S와 action A의 테이블을 업데이트 (TD이기 때문에 에피소드가 안 끝나도 바로바로 업데이트)
- Updating Action-Value Functions with Sarsa
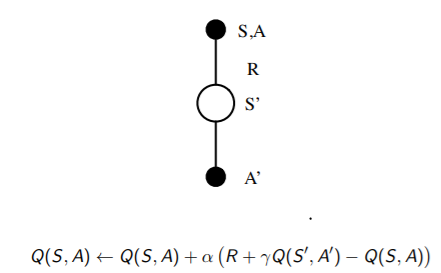
▶▶ Every time-step
Policy evaluation : Sarsa Q ≈ qπ/ Policy improvement : ε-Greedy policy improvement

◼ Sarsa의 수렴성
▫ Sarsa는 optimal action-value function에 수렴(Q(s,a) → q*(s, a))
아래 조건이 만족해야 수렴 (* 실적용할 때 사실 아래 조건 고려안 해도 수렴을 잘 한다)
- GLIE (모든 state-action pair를 방문, 결국에는 ε이 줄어들어서 greedy policy로 수렴)조건 만족
- Robbins-Monro sequence ; step-size(αt)가 Q를 먼 곳으로 데려다 줄 수 있을 만큼 크다
(αt를 무한히 더 하면 무한이 된다, αt의 제곱 합은 수렴)
- 맨 처음 episode가 끝나려면 많은 time-step이 필요하지만, reward를 얻은 경험이 쌓이면 그 지식이 활용되어, 점점 빨리 episode를 끝낼 수 있음
◼ n-Step Sarsa

◼ Forward View Sarsa(λ)
- 모든 n-step의 Q-returns들의 합 qλ
- weight (1-λ)λn-1

◼ Backward View Sarsa(λ)
- TD(λ)와 같이 online 알고리즘에서 eligibility traces 사용
- 최근에 방문 ? 여러 번 방문?
- 각 state-action pair에 대해서 Sarsa(λ)는 하나의 eligibility trace를가짐
(E0(s, a) = 0, Et(s, a) = γλEt-1(s, a) + 1(St = s, At = a) )
- TD-error δt / eligibility trace Et(s, a)
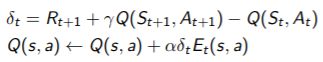
◼ Sarsa(λ) Algorithm
- 한 action을 하면 모든 s, 모든 a를 업데이트한다!!과거 지나갔던 칸도 eligibility trace가 달라지므로
- 계산량은 많아지나, 정보 전파력은 빠름
- one-step sarsa : 도착한 순간 이전 step만 업데이트
- Sarsa(λ) : 도착한 순간 지나온 모든 경로들에 대해 책임을 물어 eligibility trace 값에 비례하여 업데이트


■ Off-Policy Learning
● Off-Policy Learning
- Target policy π(a|s) ≠behaviour policy μ(a|s)
- behaviour policy μ(a|s) : 실제 (확률분포가 있어) action을 샘플링한 policy (S1,A1, R2, ... ST} ~ μ
- Target policy π evaluation - (state(v) 또는 action(q))value function 구하는것
- 왜 중요한가?
- 다른 agent를 관찰하는 것만으로도 학습 가능(사람의 경험으로 따라하는 게 아닌 최적을 찾는 것)
- old policies로 생성된 experience 재사용 가능
(On policy에서 한 번 경험을 쌓고나서 버리는 이유는 경험으로부터 policy를 업데이트하면 policy가 조금씩 바뀌기 때문. 새로운 policy로 새롭게 action을 해야 의미가 있음(target policy = behaviour policy 이므로))
- 탐험적인 행동(exploratory policy)을 하면서 동시에 optimal policy를 학습
- 한 policy를 하면서 여러 policy들을 학습할 수 있음
● Importance Sampling
- P 확률을 따르는 f(x)의 기대값으로 Q를 이용했을 때 기대값을?
- 첫번째 분포에서의 확률과 두번째 분포의 비율을 곱하여 두번째 분포를 통해 첫번째 분포를 구한다.

◼ Importance Sampling for Off-Policy Monte-Carlo
- μ(behaviour policy)로 얻은 return을 이용해 π(Target policy)를 evaluate
- policy 사이의 유사도에 따라서 return Gt를 weight
- Gt를 얻을때까지의 나왔던 모든 action의 확률의 μ와 π 비율을 곱하며 correction을 해준다.
- action 수 만큼 correction term(π/μ) 이 있음
- 상상 속에서만 존재!!! variance는 극도로 커 현실세계에서 쓸 수 없음 (특히, μ가 0일 때 쓸 수 없음)

◼ Importance Sampling for Off-Policy TD
- μ(behaviour policy)로 얻은 TD target을 이용해 π(Target policy)를 evaluate
- importance sampling에 의해 TD target에 R + ΥV(S')를 weight
- 한 step만 업데이트하므로 오직 하나의 importance sampling correction만 필요
- Monte-Carlo importance sampling보다는 variance가 작음
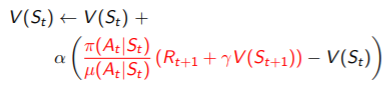
● Q-Learning
- action-value Q(s,a)를 학습하는데 off-policy learning을 고려
- importance sampling은 안 쓰고 싶음
- behaviour policy(At+1 ~ μ(•|St))에 따라 다음 action을 선택, 실제로 action을 하고 St+1에 도착.
- π를 따랐을 때 action value ? successor action A' ~ π(•|St)
- TD target에서는 다음 step에서의 Q가 사용하는데, behaviour policy 대신 target policy를 사용
- 빨간색 부분은 다음 state인 st+1에서 어떤 action을 할건데 그 action을 했을 때 value guess(bootstrapping)
- 실제 behaviour policy를 사용하는 것이 아닌 학습하고자 하는 policy인 target policy로 action을 하나 뽑아 그 value를 사용
- guess이므로 실제 하지 않고 계산만 하면 된다.!! At+1가 아닌 A'으로!

◼ Off-Policy Control with Q-Learning
- behaviour policy를 하나 정함
- behaviour policy도 target policy처럼 계속 improve
▫ Target policy π : greedy로 정함 Q(s, a)

▫ Behaviour policy μ : ε-greedy로 정함 Q(s, a)
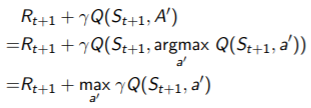

▫ Q-Learning은 optimal action-value function에 수렴(Q(s,a) → q*(s, a))

■ Summary
- Control : 최적의 policy를 찾는 것
- Sarsa : Model Free / Conrol / On Policy
- Q-Learning : Model Free / Control / Off Policy
 |
 |
| Sarsa | Q-Learning |
 |
 |
'Data Science&AI' 카테고리의 다른 글
| [Object Detection] 1. Object Detection이란? (0) | 2022.02.21 |
|---|---|
| [강화학습 논문리뷰] DQN(Deep Q-Network) 소개 (0) | 2022.02.09 |
| [강화학습 뿌시기] 4. Model-Free Prediction (1) | 2022.01.24 |
| [강화학습 뿌시기] 3. Planning by Dynamic Programming (0) | 2022.01.08 |
| [강화학습 뿌시기] 2. Markov Decision Processes(MDP) (0) | 2022.01.07 |
- Total
- Today
- Yesterday
- 모델 드리프트 대응법
- 모델 배포
- 오토인코더
- 생성형BI
- data drift
- 비즈니스 관점 AI
- pandas-gpt
- NHITS설명
- Data Drift와 Concept Drift 차이
- AutoEncoder
- amazon Q
- amzaon quicksight
- 추천시스템
- pandas-ai
- 영어공부
- Concept Drift
- Model Drift
- 데이터 드리프트
- Model Drift Detection
- 모델 드리프트
- SQLD 정리
- Tableau vs QuickSight
- 시계열딥러닝
- 영화 인턴
- On-premise BI vs Cloud BI
- SQLD자격증
- SQLD
- Generative BI
- Data Drift Detection
- 최신시계열
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 27 | 28 | 29 | 30 | 31 |
