티스토리 뷰
이 글은 David Silver의 강화학습 강의자료를 기초로 하였으며 아래의 강의를 듣고 작성하였습니다.
https://www.youtube.com/watch?v=rrTxOkbHj-M
https://www.davidsilver.uk/teaching/
Teaching - David Silver
www.davidsilver.uk
Synchronous Dynamic Programming (Full-width Backups(Policy Evaluation, Policy Iteratoin, Value Iteration)) / Asynchronous Dynamic Programming (Full-width Backups)
■ Dynamic Programming
● Dynamic Programming이란?
- Dynamic : sequential or temporal component to the problem
- Programming : program을 최적화시키는 것 (policy)
- 복잡한 문제를 푸는 방법론
- 큰 문제를 작은 문제로 나누고, 작은 문제에 대한 솔루션을 찾고 그 솔루션을 다 모아 큰 문제를 푸는 것
- Model-based 강화학습 문제에서 쓰임
(* Model-based : Environemt에 대한 정보가 있어 어떤 action을 할 때 어떤 state에 도착할지 알 수 있음,
Model-free : Environment에 대한 완전한 정보가 없음)
● Dynamic Programming의 요건
(1) Optimal substructure : optimal 솔루션이 작은 문제로 나눌 수 있어야 함
(2) Overlapping subproblems : 한 subproblem들이 여러 번 등장하여, 그 솔루션을 캐쉬해 뒀다가
다시 사용할 수 있음
- Markov decision process가 이 2조건을 만족!
- 벨만 방정식은 recursive decomposition을 할 수 있고(subproblem으로 나누는 것)
- value function은 솔루션들을 저장하고 다시 사용 가능)
→ MDP를 풀 때 Dynamic programming을 적용할 수 있음
● Planning by Dynamic Programming
- MDP에 대한 full knowledge를 가정한다.
- planning : 모델을 알 때(MDP에 대한 full knowledge가 있을 때) MDP를 푸는 것(최적의 Policy를 찾는 것)
- Prediction / Control
(1) Prediction :
- Value function을 맞추는 것
- Input : MDP(S(state집합), A(action집합), P(transition matix), R(state들의 reward집합), r(discount factor)) and policy (or MRP)
(2) Control :
- Optimal policy(+ optimal value function)를 찾는 것
- Input : MDP(S, A, P, R, r)
● Dynamic Programming의 적용 사례
- Scheduling 알고리즘, String 알고리즘(e.g. sequence alignment), Graph 알고리즘(e.g. shortest path 알고리즘), Graphical models(e.g. Viterbi 알고리즘), Bioinformatics(e.g. lattice models)
■ Policy Evaluation (Prediction)
- Policy가 고정되었을 때, value function을 찾는 것 (Policy를 따라갔을 때 return이 얼마인가)
- Problem : 주어진 policy에 대한 평가
Solution : iterative application of Bellman expectation back up
(* back up : cache ,잠시 메모리에 저장)
- synchronous backups(모든 단계에 대해 한단계 한번씩) 다음 state들의 value를 이용해 업데이트
| - 각 iteration k+1에서 - 모든 states s ∈ S 들에 대해서 - vk(s')에서 vk+1(s)로 업데이트 (Bellman expectation 이용, 모든 칸들의 값들을 업데이트) - s' : state s의 다음 state |
▶ S의 값들을 좀 더 정확하게 업데이트, 다음 state들의 value값들을 이용하여 업데이트 하는 것!
(v1 → v2 → .... → vπ 에 수렴(값이 안 바뀜))

e.g. Evaluating a Random Policy in the Small Gridworld (Evaluation하는데 Optimal한...!)
- Prediction문제이므로 MDP와 Policy가 주어짐, (Nonterminal) state가 14개, terminal state 1개
- 4분의 1 확률로 상하좌우 움직임
- reward : -1 (terminal state 도달할 때까지), discount factor : 1(undiscounted)
k=2의 (2,2) : Reward(-1) + 1*(1/4)*(-1)*4
(3,4) : Reward(-1) + 1*(1/4)*(-1)*3 + 1*(1/4)*0
 |
|
 |
 |
- 각 state에서 바보같은 Random Policy를 평가하는데, Grid하게(다음 칸 중에 제일 좋은 쪽으로) 움직이면 Optimal policy를 찾을 수 있다. 무한히 갈 필요 없다.
■ Policy Iteration (Control)
● How to Improve a Policy
- Policy π가 주어졌을 때
(1) Policy π를 Evaluate (vπ를 추정, iterative policy evaluation)

(2) vπ에 따라 greedy하게 acting하며 policy를 Improve

- small gridworld : imporoved policy = optimal (π' = π*) evaluation하면 바로 imporve됨
- 일반적으로는 모든 interation에서 imporvement/evaluation을 반복해야 한다.
- policy iteration과정에서 항상 π*로 수렴
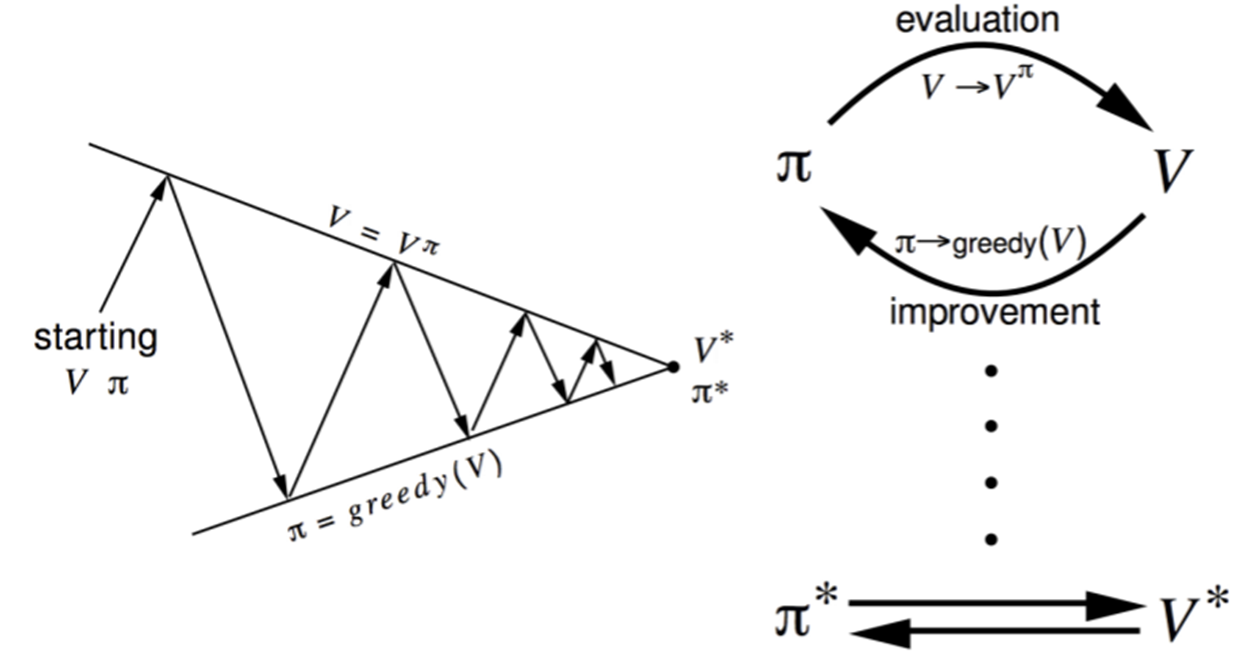
● Policy Improvement
- deterministic policy a= π(S)
- Q에 대해 greedy하게 움직일 때 policy을 개선(π보다는 π'이 낫다)할 수 있다.

(1) state s에서 다음 한 스텝을 넘어갈 때 value를 개선시킴
* q : action-value function ( s에 있을 때 π로 action을 하나 골라)
* vπ(s) = qπ(S, π(S)) :
- s로부터 π를 따라가나 s에서 π가 골라준 action을 하나 하고 그 뒤로 π를 따라가나 value는 같다
* qπ(S, π(S))
- s에서 어떤 action을 한 것의 qπ는 s에서 할 수 있는 모든 action 중에 가장 qπ가 높은값 보다는 같거나 낮다
- 첫 스텝은 π'을 따라 한 action을 하고 그 이후는 π를 따라가는 것의 value qπ(S, π'(S)) 는
첫 스텝과 그 이후 스텝에서 π를 따라갈 때 value qπ(S, π(S)) 것 이상이다.
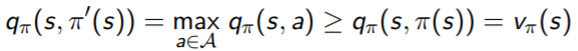
(2) 따라서 Value function은 vπ'(s) ≥ vπ(s)로 개선
(모든state들에 대해 π일 때 value보다 π'일 때 value가 높아서 greedy하게 움직이는 게 value 개선됨)

(3) Improvements stop (벨만 Optimality equation만족) → Vπ(s) = V*(s) , π : optimal policy

● Modified Policy Iteration
- Policy evaluation하는데 꼭 Vπ에 수렴할 때까지 해야 하는가?
- 아니면 stopping condition을 도입?
- 단순히 k iteration을 한 후에 stop해도 되는가?(small gridworld는 k=3이 충분한 optimal policy 얻을 수 있음)
- Why not update policy every iteration? (i.e. stop after k=1(한 번 평가하고 greedy)) : value iteration과 동일
■ Value Iteration (Control)
● Principle of Optimality
- optimal policy는 2요소로 나뉨
- A* : optimal first action
- 그 action을 해서 다음 state S'에 도달. 거기서부터 최적의 policy를 따름

● Deterministic Value Iteration
- S'의 솔루션을 알면 S의 솔루션을 알 수 있다.
- subproblem에 대한 솔루션 V*(S')을 알면 (S' : S에서 갈 수 있는 state들)
- 한 스텝 lookahead를 통해 솔루션 V*(S)을 구할 수 있음 (벨만 optimality equation)
- max로 엮여 역행렬로 못 풀고 iterative하게 업데이트를 해야 함

- 직관적으로 Start with final rewards & work backwards! (terminal에 가까운 것부터 확정)
- Policy evaluation는 없고, value만 iteration!
e.g) Shortest Path

● Value Iteration
- Problem : optimal policy 찾기
Solution : iterative application of Bellman optimality backup
- v1 → v2 → .... → v* 에 수렴(값이 안 바뀜)
- synchronous backups(모든 단계에 대해 한단계 한번씩) 다음 state들의 을 이용해 업데이트
| - 각 iteration k+1에서 - 모든 states s ∈ S 들에 대해서 - vk(s')에서 vk+1(s)로 업데이트 (Bellman expectation 이용, 모든 칸들의 값들을 업데이트) |
- explicit한 policy가 없다.
- value iteration을 도는데 중간중간 value function들은 어떤 policy의 value도 아니다.
| Problem | Bellman Equation | Algorithm |
| Prediction | Bellman Expectation Equation | Iterative Policy Evaluation |
| Control | Bellman Expectaton Equation + Greedy Policy Improvement |
Policy Iteration |
| Control | Bellman Optimality Equation | Value Iteraton |
- 알고리즘은 state-value function에 기초
- 각 iteration에서 복잡도 : O(mn2) (m : actions, n : states)
- action-value function을 적용할 수 있음
■ Asynchronous Dynamic Programming
- 이제까지는 synchronous backup을 이용 (모든 states들이 parallel하게 back up)
- Asynchronous DP : 독립적으로 또는 순서를 다르게 state들을 back up,
- 각각의 선택된 state들에 대해서만 backup 적용
- computation을 줄일 수 있고
- converge를 보장(여러 state들이 골고루 뽑혀야 함)
(1) In-place dynamic programming : value function을 오직 한 copy(array)만 갖고 있음
(* synchronous value iteration : 두 copy value function을 저장(new/old value function),
이전 step에서 방금 업데이트된 value function정보만 이용

(2) Prioritised sweeping : state value 업데이트할 때 벨만 에러 크기를 이용하여 중요한 순서부터!
- 벨만 에러가 크면 중요한 애들부터 업데이트

(3) Real-time dynamic programming : state가 넓고 agent가 가는 state는 한정적일 때, agent가 방문한 state들을 먼저 update

■ Full-Width Backups
- DP는 full-width backup 이용
- 각 backup에서(sync or async)
- 모든 다음 state, action이 고려
- MDP transition들과 reward function에 대한 지식을 이용
- DP는 medium-sized problem에 효과적(millions of states)
- 큰 문제에서는 차원의 저주에 빠져 DP를 적용할 수 없음 (state가 늘어날 수록 state variables 수는 지수적으로 늘어난다)
■ Sample Backups
- sample rewards, sample transition을 이용 (reward function과 transition dynamics 대신에)
- 장점 :
- Model-free : 미리 MDP에 대한 지식을 알 필요가 없음
- sampling을 통하여 차원의 저주를 깸
- backup의 cost는 constant
'Data Science&AI' 카테고리의 다른 글
| [강화학습 뿌시기] 5. Model Free Control (0) | 2022.02.01 |
|---|---|
| [강화학습 뿌시기] 4. Model-Free Prediction (1) | 2022.01.24 |
| [강화학습 뿌시기] 2. Markov Decision Processes(MDP) (0) | 2022.01.07 |
| [강화학습 뿌시기] 1. 강화학습(Reinforcement Learning) 기초 (0) | 2022.01.06 |
| [논문리뷰]Tabular Data : DeepLearning is Not All You Need (0) | 2021.07.28 |
- Total
- Today
- Yesterday
- Model Drift Detection
- SQLD자격증
- 모델 배포
- SQLD
- Tableau vs QuickSight
- On-premise BI vs Cloud BI
- 모델 드리프트
- 오토인코더
- data drift
- Data Drift Detection
- 모델 드리프트 대응법
- 비즈니스 관점 AI
- 최신시계열
- pandas-gpt
- 영화 인턴
- amazon Q
- 데이터 드리프트
- SQLD 정리
- 생성형BI
- Concept Drift
- 시계열딥러닝
- amzaon quicksight
- pandas-ai
- Generative BI
- 영어공부
- Data Drift와 Concept Drift 차이
- Model Drift
- AutoEncoder
- 추천시스템
- NHITS설명
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | ||||
| 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| 25 | 26 | 27 | 28 | 29 | 30 | 31 |
